Problem 91 - Right triangles with integer coordinates
The points P (x1, y1) and Q (x2, y2) are plotted at integer co-ordinates and are joined to the origin, O(0,0), to form ΔOPQ.
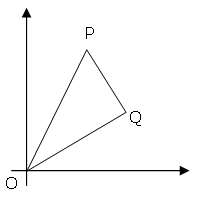
There are exactly fourteen triangles containing a right angle that can be formed when each co-ordinate lies between 0 and 2 inclusive; that is,
0 ≤ x1, y1, x2, y2 ≤ 2.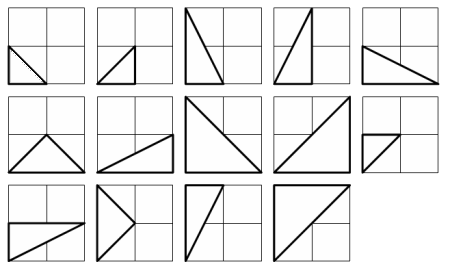
Given that 0 ≤ x1, y1, x2, y2 ≤ 50, how many right triangles can be formed?
Right Triangle Locations
I think upon first reading this problem, most people would begin to look for patterns in the fourteen triangle solutions shown. Doing this, I noticed that you could divide these triangles into three groups depending on where the right angle falls, either: (1) at the origin, (2) on the x- or y-axis, or (3) any other point.
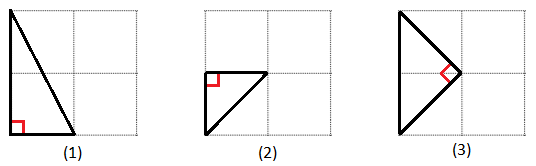
For class one triangles, we can choose any 2 points, one on the x-axis and the other on the y-axis (both ≥ 1), and the resulting triangle will be a valid right triangle. The total number of combinations of these 2 points is N×N (where N is the grid size). Therefore the number of triangle solutions with the right angle at the origin = N×N.
For the second class of triangles, it's pretty easy to see that for any given point on one axis, there are N valid right triangles, one for each point ≥ 1 on the other axis. For example, triangle (2) above has a right angle at (0, 1) and solution triangles with a right angle located there could have a third point at (1, 1), (2, 1), (3, 1), ... up to (N, 1).
The challenge for this problem, then, comes down to finding all right triangles of the third type. It was here I needed to break out Pythagoras.
Pythagorean Theorem
Given some arbitrary point (a, b) for a ≥ 1 and b ≥ 1, we can use the Pythagorean theorem to find some other point (x, y) that, with a point at the origin, forms a right triangle with right angle at (a, b).
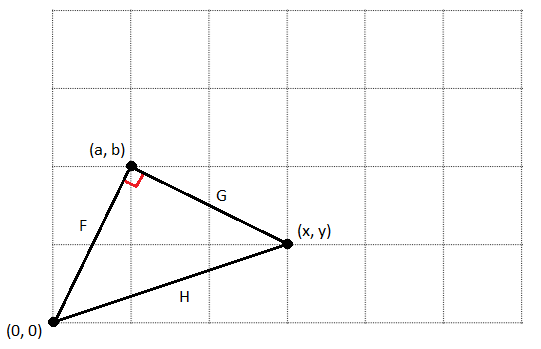
For
\(F = \sqrt{a^2+b^2}\)
\(G = \sqrt{(a-x)^2+(b-y)^2}\)
\(H = \sqrt{x^2+y^2}\)
the Pythagorean theorem gives:
\(F^2+G^2 = H^2\)
\((\sqrt{a^2+b^2})^2+(\sqrt{(a-x)^2+(b-y)^2})^2 = (\sqrt{x^2+y^2})^2\)
\(a^2+b^2+(a-x)^2+(b-y)^2 = x^2+y^2\)
\(a^2+b^2+a^2-2ax+x^2+b^2-2by+y^2 = x^2+y^2\)
\(2a^2+2b^2-2ax-2by = 0\)
\(ax+by = (a^2+b^2)\)
For a given point (a, b), this turns into a linear Diophantine equation with two unknowns, x and y. Solving this equation for x and y in the range [0, N] will give all right triangles with right angle at (a, b). To find all these pairs we'll first find an initial solution (x0, y0) to the equation. From that solution we can generate all other solutions.
Finding an Initial Solution
Bézout's Identity states that for integers a and b with greatest common divisor d, there are integers s and t (called Bézout's coefficients) that satisfy
\(s \cdot a+t \cdot b = d\)
This also means that there are only solutions to
\(ax+by = (a^2+b^2)\)
if (a2 + b2) divides d. Using the extended Euclidean algorithm, we can calculate the gcd of a and b as well as Bézout's coefficients s and t:
extendedEuclidean(a, b)
(1) Initialize the Bézout coefficient (s) and remainder (r)
s = 0, s_prev = 1
r = b, r_prev = a
(2) While (r ≠ 0)
(i) Calculate the quotient
quotient = floor(r_prev / r)
(ii) Update s and r
(r, r_prev) = (r_prev - quotient*r, r)
(s, s_prev) = (s_prev - quotient*s, s)
(3) Set the Bézout coefficients
t = (b == 0) ? 0 : floor((r_prev - s_prev*a) / b)
s = s_prev
(4) Set the gcd (d)
d = r_prev
(4) Return d, s, t
From s and t, an initial solution (x0, y0) follows:
\(x_0 = s \cdot \frac{(a^2+b^2)}{d}\)
\(y_0 = t \cdot \frac{(a^2+b^2)}{d}\)
Generating all Solutions
For any linear Diophantine equation, the existence of one solution implies the existence of an infinite amount of solutions. All other solutions are given by
\((x, y) = (x_0+k\cdot\frac{b}{d}, y_0-k\cdot\frac{a}{d})\)
where \(d = gcd(a, b)\), \(k\) is an arbitrary integer
The initial solution calculated above does not necessarily contain positive integers. To solve this problem we need to find which values of k produce values of x and y ≥ 0. To find these values of k, rearrange the above equations for x and y and solve both for k.
\(x = x_0+k\cdot\frac{b}{d} \geq 0\)
\(k \geq -x_0\cdot\lfloor\frac{d}{b}\rfloor\)
and
\(y = y_0-k\cdot\frac{a}{d} \geq 0\)
\(k \leq y_0\cdot\lfloor\frac{d}{a}\rfloor\)
Now we only need to check which produce values of x and y in the range [0, N] (excluding the solution (x, y) = (a, b)) to find all solution triangles of the third case.
Implementation
First, a function for the extended Euclidean algorithm:
int extendedEuclideanGCD(int a, int b, int &bezout_s, int &bezout_t) {
// compute the gcd of (a, b) and the Bezout coefficients s and t such that a*s + b*t = gcd(a, b)
int r_prev = std::abs(a), r = std::abs(b);
int s_prev = 1, s = 0;
while (r != 0) {
int q = r_prev / r;
int temp = r_prev;
r_prev = r;
r = temp - q*r;
temp = s_prev;
s_prev = s;
s = temp - q*s;
}
bezout_s = s_prev;
bezout_t = (b == 0) ? 0 : (r_prev-a*s_prev)/b;
return r_prev;
}This function returns the gcd of a and b directly and returns bezout_s and bezout_t by reference.
Then, a function to find the initial solution (x0, y0):
bool findInitialSolution(int a, int b, int &x0, int &y0, int &d) {
d = extendedEuclideanGCD(a, b, x0, y0); // a*bezout_s + b*bezout_t = d
int c = a*a + b*b;
if (d == 0 || c % d != 0) return false; // no solutions if (a^2+b^2) doesn't divide d
x0 *= c/d; // x0 = bezout_s * (a^2+b^2)/d
y0 *= c/d; // y0 = bezout_t * (a^2+b^2)/d
return true;
}Here, the initial solution is returned by reference (x0, y0) along with the gcd, d. The function returns true if solutions exist for (a, b) and false if not.
The main function countSolutions returns how many right triangles exist in an n×n grid with right angle located at (a, b).
int countSolutions(int a, int b, int n) {
if (a == 0 && b == 0) return n*n; // n^2 solutions at the origin
else if (a == 0 || b == 0) return n; // n solutions when (a, b) is on the x or y axis
// Get the gcd(a,b) and an initial solution
int x0 = 0, y0 = 0, d = 0;
if (!findInitialSolution(a, b, x0, y0, d)) return 0;
/*
All other solutions are generated from the initial solution by:
x = x0 + k*(b/d)
y = y0 - k*(a/d)
for any integer k. Solve for the min and max values of k that give positive solutions for (x, y)
*/
int minK = -x0 * d/b;
int maxK = y0 * d/a;
int count = 0;
for (int k = minK; k <= maxK; k++) {
int x = x0 + k * b/d;
int y = y0 - k * a/d;
if (x > n || y < 0) break; // while k increases, x increases and y decreases
if (x == a && y == b) continue; // (x, y) must be a new point
if (x >= 0 && y <= n) count++;
}
return count;
}Lastly, the driver function:
int numRightTriangles(int n) {
int count = 0;
for (int a = 0; a <= n; a++) {
for (int b = 0; b <= n; b++) {
count += countSolutions(a, b, n);
}
}
return count;
}