Custom Board Editor

A
B
C
1
2
3
1
2
3
4
5
6
7
8
9
1
2
3
4
5
6
7
8
9
1
2
3
4
5
6
7
8
9
1
2
3
4
5
6
7
8
9
1
2
3
4
5
6
7
8
9
1
2
3
4
5
6
7
8
9
1
2
3
4
5
6
7
8
9
1
2
3
4
5
6
7
8
9
1
2
3
4
5
6
7
8
9
4
5
6
1
2
3
4
5
6
7
8
9
1
2
3
4
5
6
7
8
9
1
2
3
4
5
6
7
8
9
1
2
3
4
5
6
7
8
9
1
2
3
4
5
6
7
8
9
1
2
3
4
5
6
7
8
9
1
2
3
4
5
6
7
8
9
1
2
3
4
5
6
7
8
9
1
2
3
4
5
6
7
8
9
7
8
9
1
2
3
4
5
6
7
8
9
1
2
3
4
5
6
7
8
9
1
2
3
4
5
6
7
8
9
1
2
3
4
5
6
7
8
9
1
2
3
4
5
6
7
8
9
1
2
3
4
5
6
7
8
9
1
2
3
4
5
6
7
8
9
1
2
3
4
5
6
7
8
9
1
2
3
4
5
6
7
8
9
D
E
F
1
2
3
4
5
6
7
8
9
1
2
3
4
5
6
7
8
9
1
2
3
4
5
6
7
8
9
1
2
3
4
5
6
7
8
9
1
2
3
4
5
6
7
8
9
1
2
3
4
5
6
7
8
9
1
2
3
4
5
6
7
8
9
1
2
3
4
5
6
7
8
9
1
2
3
4
5
6
7
8
9
1
2
3
4
5
6
7
8
9
1
2
3
4
5
6
7
8
9
1
2
3
4
5
6
7
8
9
1
2
3
4
5
6
7
8
9
1
2
3
4
5
6
7
8
9
1
2
3
4
5
6
7
8
9
1
2
3
4
5
6
7
8
9
1
2
3
4
5
6
7
8
9
1
2
3
4
5
6
7
8
9
1
2
3
4
5
6
7
8
9
1
2
3
4
5
6
7
8
9
1
2
3
4
5
6
7
8
9
1
2
3
4
5
6
7
8
9
1
2
3
4
5
6
7
8
9
1
2
3
4
5
6
7
8
9
1
2
3
4
5
6
7
8
9
1
2
3
4
5
6
7
8
9
1
2
3
4
5
6
7
8
9
G
H
I
1
2
3
4
5
6
7
8
9
1
2
3
4
5
6
7
8
9
1
2
3
4
5
6
7
8
9
1
2
3
4
5
6
7
8
9
1
2
3
4
5
6
7
8
9
1
2
3
4
5
6
7
8
9
1
2
3
4
5
6
7
8
9
1
2
3
4
5
6
7
8
9
1
2
3
4
5
6
7
8
9
1
2
3
4
5
6
7
8
9
1
2
3
4
5
6
7
8
9
1
2
3
4
5
6
7
8
9
1
2
3
4
5
6
7
8
9
1
2
3
4
5
6
7
8
9
1
2
3
4
5
6
7
8
9
1
2
3
4
5
6
7
8
9
1
2
3
4
5
6
7
8
9
1
2
3
4
5
6
7
8
9
1
2
3
4
5
6
7
8
9
1
2
3
4
5
6
7
8
9
1
2
3
4
5
6
7
8
9
1
2
3
4
5
6
7
8
9
1
2
3
4
5
6
7
8
9
1
2
3
4
5
6
7
8
9
1
2
3
4
5
6
7
8
9
1
2
3
4
5
6
7
8
9
1
2
3
4
5
6
7
8
9

About

The solver was written in C++ and compiled to Webassembly using Emscripten. The GUI was written in Javascript. Both the original C++ source code and javascript can be found on my Github.

Using the solver

Sudoku is a logic puzzle game played on a 9x9 grid of cells. The objective is to fill each row, each column, and each 3x3 sub-grid (box) with the numbers 1-9. The only rule is that no number can appear more than once in any row, column, or box. Although you can arrive at the solution through guessing, the purpose of the game is to find cell solutions through logical deductions.

Entering data - Solutions can be entered or removed using a keyboard or the Digit input mode next to the board. In the process of solving, it's often helpful to write possible solutions into a cell before you know the true solution. Also known as pencil marks, these mini-numbers can be entered while Candidate mode is selected.

Custom puzzles - To enter a custom puzzle, first select Custom from the puzzle dropdown. Then, any number of given cell solutions (or clues) and candidates can be entered manually as described above. Alternatively, puzzle clues can be entered as an 81 character string in the Custom Board Editor. For unsolved cells in this string, any character other than 1-9 may be used (common characters are . or 0).

Solving - The solver works by applying a predetermined order of strategies (described below) until some change is made to the board, displaying the results, and then starting the strategy list over from the beginning. The Step button will show the result of one successful strategy at a time while the Solve button will find and display all the steps needed to solve the puzzle. Any change made can also be undone with the Undo button. For the most difficult puzzles, the solver may run out of strategies in which case the solved puzzle (if it exists) will be found by a fast brute force search.

Strategies

First, a brief explanation of the terminology used in the following strategies:

  • Cell - one of the 81 squares that make up the sudoku board
  • Box - a grid of 3x3 cells that must contain the digits 1-9
  • Unit - a group of cells that must contain the digits 1-9; i.e., a row, a column, or a box
  • Candidate - a possible solution to a cell, marked on the board as a smaller number

naked single, hidden single

This simple strategy comes in two types. A naked single appears when a candidate is the only possible number left in a cell. Conversely, a hidden single is when there is only one possible cell left for a candidate. Or said another way, if candidate k can only be in one cell within a row, column, or box, k is a hidden single.

Singles are the bread and butter of sudoku solving strategies and are always the first thing you should look for. These two strategies alone are enough to solve nearly all "easy" and many "intermediate" level puzzles.

naked pair/triplet/quad, hidden pair/triplet/quad, pointing pair/triplet, box/line reduction, x-wing, swordfish, jellyfish

Also known as locked sets, the remainder of the simple strategies can all be described by a common line of reasoning:

If there is a set of n X's and n Y's in Z, any other X's in those n Y's can be removed

where X, Y, and Z are some combination of row/column/box/cell/candidate and n is the size of the subset

These subset strategies can be broken into four groups:

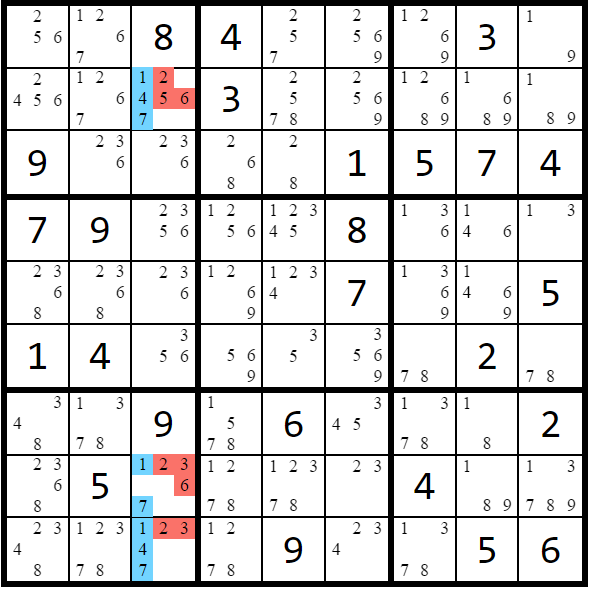
Naked subset - If there are n cells containing only n candidates in a unit, then those n candidates can be removed from other cells in that unit.

Naked subsets can come as pairs, triplets, or quads, corresponding to n = 2, 3, 4. For triplets or quads, it is not necessary for every cell to contain every candidate; only that the total number of cells and candidates equals 3 or 4 (as shown in the naked triplet example).

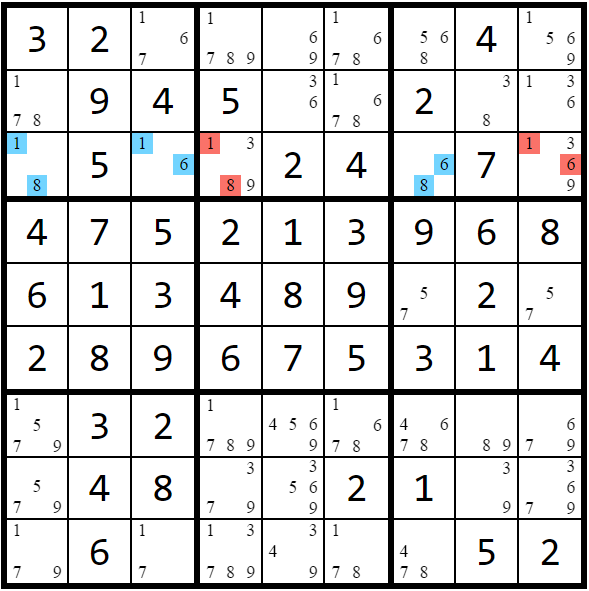
Naked triplet - In the third row, there are 3 cells that in total contain 3 candidates (colored blue); 1, 6, and 8 must go in those cells and so can be removed from other cells in that row

Hidden subset - If there are n candidates within only n cells in a unit, then any other candidates in those n cells can be removed.

The same naming conventions listed above also apply to hidden subsets.

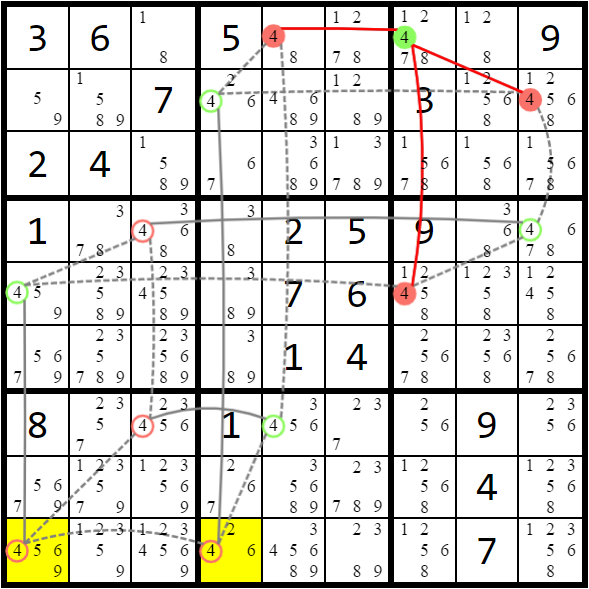
Hidden triplet - In the third column, there are 3 candidates (colored blue) that can only be found in the same 3 cells; 1, 4, and 7 must go in those cells and so the other candidates (colored red) can be removed

Fish subset

(Type 1) If there are n rows where n columns contain a candidate, that candidate can be removed from any other rows in those n columns.

(Type 2) If there are n columns where n rows contain a candidate, that candidate can be removed from any other columns in those n rows.

These formations have different names depending on their size n:

  • n = 2 ⇒ X-Wing
  • n = 3 ⇒ Swordfish
  • n = 4 ⇒ Jellyfish
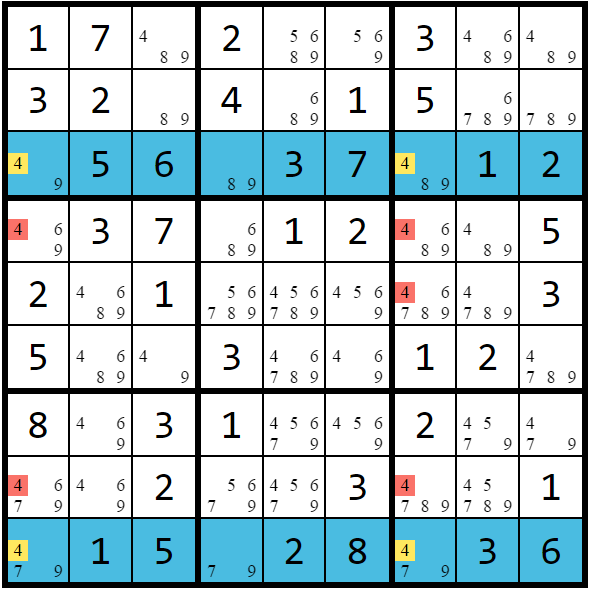
X-Wing (Type 1) - In the 2 blue rows, candidate 4 can only be placed in 2 columns (column 1 and column 7); the other cells in those 2 columns cannot contain a 4

Intersection subset

(Pointing) If a candidate appears in only n cells in a box and those cells are all in the same row/column, that candidate can be removed from the other cells in that row/column.

(Box/line) If a candidate appears in only n cells in a row/column and those cells are all in the same box, that candidate can be removed from the other cells in that box.

Intersection subsets can only have a size of n = 2 or n = 3 because a box can only have 3 cells at most aligned on the same row or column.

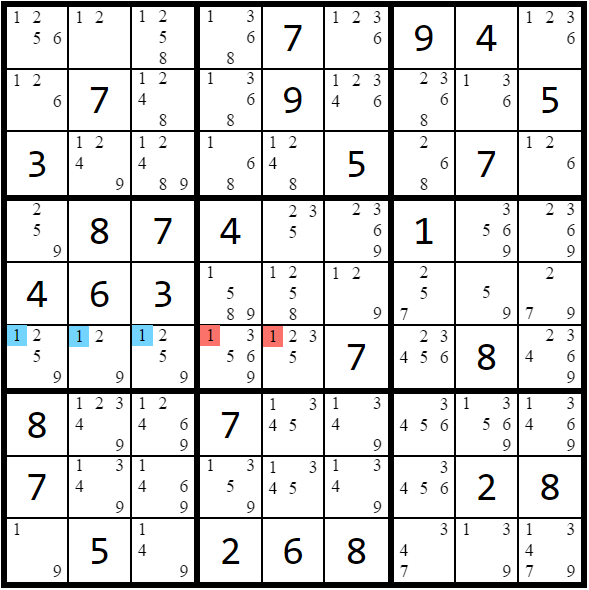
Pointing triple - In the 4th box, candidate 1 can only be on the 6th row (colored blue); the other cells in that row cannot contain a 1

y-wing, xyz-wing, wxyz-wing

Bent sets are essentially naked subsets "bent" onto two different units. They consist of n cells containing only n candidates where the cells belong to 2 different units. The 2 units must be different types and at least 1 cell must be present in both units. The cell(s) that are part of both units are the hinge cells.

Under certain conditions a bent set can be treated like a naked set where the n candidates must all appear in some combination in the n cells of the set:

(Type 1) If exactly 1 of the n candidates in the bent set is present in 2 separate units, that candidate can be removed from any cells outside the bent set that can "see" all instances of that candidate in the bent set.

(Type 2) If none of the n candidates in the bent set are present in 2 separate units, all of the n candidates in the bent set can be removed from any cells outside the bent set that "see" all instances of each candidate in the bent set.

Type 1 bent sets appear far more often. Both types of bent sets can be referred to by their size similar to naked/hidden sets (bent triplet, bent quad, bent quint). They have also been given the following names:

  • n = 3 ⇒ Y-Wing (when the hinge cell contains 2 of the 3 candidates)
  • n = 3 ⇒ XYZ-Wing (when the hinge cell contains all 3 candidates)
  • n = 4 ⇒ WXYZ-Wing
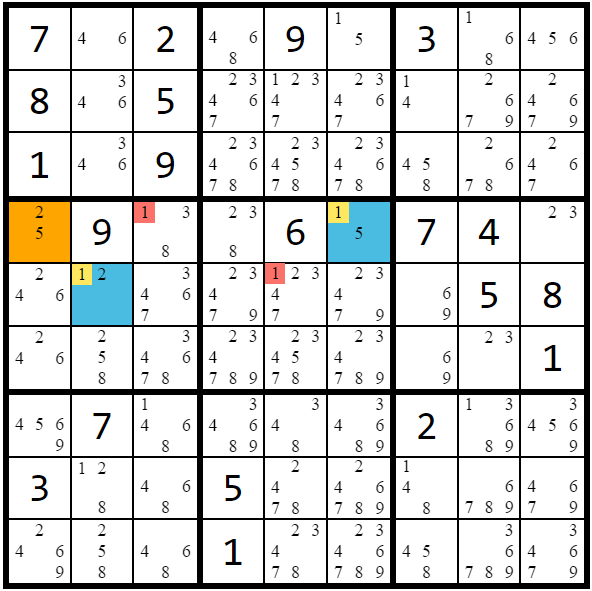
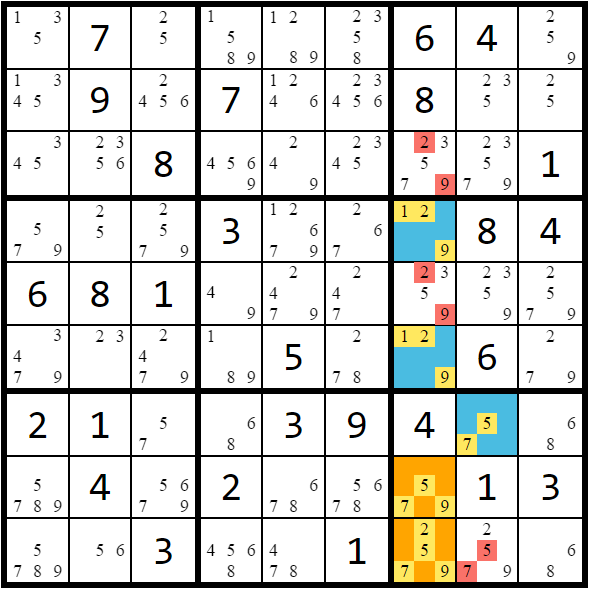
Y-Wing (Type 1) - The 3 shaded cells of the bent triple lie on row 4 and box 4 with the single hinge cell shaded orange. Within the bent set, only one candidate, 1, falls on the two different units. Therefore one of the 1's (colored yellow) must be a cell solution. The 1's outside the bent set (colored red) that "see" both yellow 1's can be removed.
Bent quint (Type 2) - The 5 shaded cells lie on column 7 and box 9 with the two hinge cells shaded orange. Within the bent set, every candidate is restricted to a single unit (either column 7 or box 9). Therefore, 1, 2, 5, 7, and 9 must appear in some combination in the shaded cells. Any other candidate outside the bent set that can see all occurrences in the bent set can be removed (colored red).

simple coloring, 3D-medusa coloring

The coloring strategy introduces the more general chaining strategies. Imagine that a row has only 2 possible cells for candidate k. If the first cell IS k in the board's solution, then the second cell CANNOT be k. It is also equally valid to say that if the first cell is NOT k then the second cell MUST be (since there must be a k in this row). These two candidate possibilities are fundamentally linked.

By finding and connecting all of these strong links between candidates, we can create a connected graph of vertices. Coloring these vertices alternating between two colors will then represent the two possible outcomes the graph could resolve to in the board's solution.

There are 2 types of these graphs. Simple coloring describes a graph that is built on a single candidate k. 3D-Medusa refers to a graph that contains any of the candidates from 1-9. 3D-Medusa coloring requires another type of strong link: when a single cell contains only 2 candidates, those 2 candidates can be connected with a strong link using the same reasoning given above.

With either type of graph, there are two ways to find eliminations:

(Rule 1) If any uncolored candidate on the board can "see" both colors of the graph, that candidate isn't possible in either outcome and can be removed.

(Rule 2) If all candidates in a cell can "see" color A, OR if all occurrences of candidate k in a unit can "see" color A, all candidates colored A can be removed and all candidates colored B are the solutions to their cell.

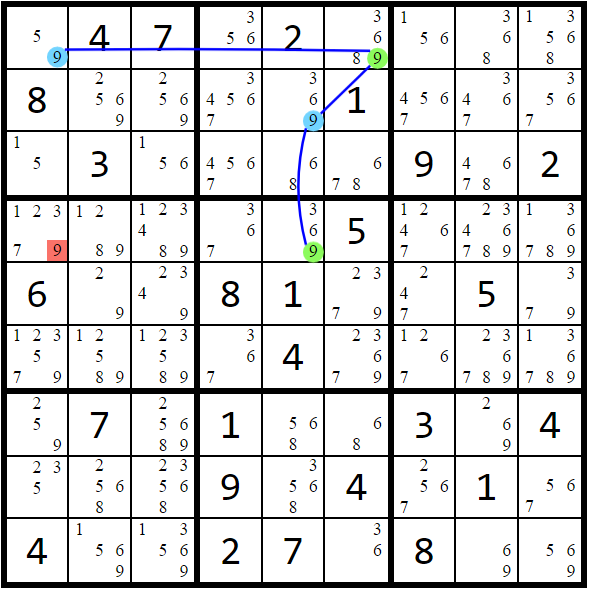
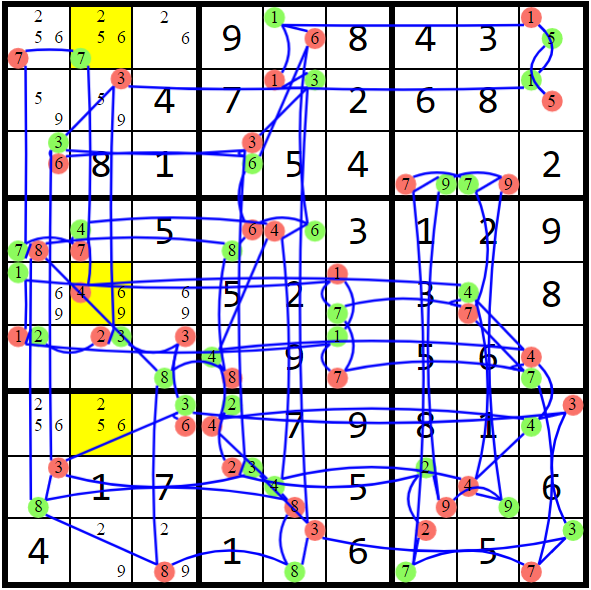
Simple coloring (rule 1) - Several strong links between occurrences of candidate 9 have been drawn and colored. In the board's solution, either all of the green 9's are solutions or all of the blue 9's are solutions. In either case the candidate colored in red cannot be possible, so it can be removed.
3D-Medusa coloring (rule 2) - All of the 6's in column 2 (located in the yellow cells) can "see" a red colored candidate (in the top and bottom yellow cells there is another red 6 in the same row; in the middle yellow cell there is a red 4 in the same cell). If red was the solution to the board, column 2 would not contain a 6. Therefore green must be the solution and all red candidates can be removed.

alternating inference chain, x-cycle

As previously described, a strong link between candidates has only 2 possible outcomes in the board's solution. When multiple candidates are connected with strong links, that group of candidates forms a strongly-linked chain. The chain as a whole also has only two possible outcomes. Coloring strategies only consider one strongly-linked chain at a time when searching for eliminations. We can take chaining strategies further by introducing weak links to our graph.

Any two candidates that "see" each other and don't form a strong link instead form a weak link. Like strong links, if one end of the weak link IS the cell solution, the other CANNOT be. However, the inverse is not true: if one end is NOT the cell solution, we can't make any inferences about the other end.

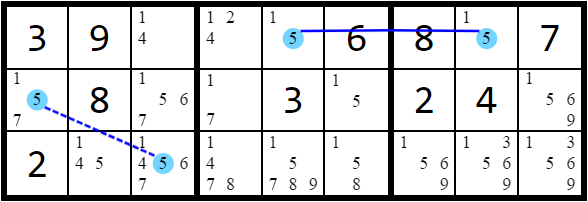
Weak links are shown with a dotted line (left) and strong links with a solid line (right)

With weak links we can connect several strongly-linked chains together and make more inferences. The same rules in Coloring above also apply to alternating inference chains:

(Rule 1) If both possible outcomes of a chain lead to a candidate being "turned off", that candidate can be eliminated.

This contradiction produces a pattern consisting of a cycle of alternating strong/weak links that contains two weak links adjacent to the eliminated candidate. Logically, you can interpret the cycle as saying "if candidate k is the solution to its cell, the links of the cycle imply it must not be the solution". This works because "turning on" k results in the other end of the adjacent weak link being "turned off." That "off" candidate then implies the candidate at the other end of the next (strong) link must be "turned on". These inferences alternate around the cycle back to k and work in either direction. The resulting contradiction allows us to remove k.

When a cycle with these properties consists of only one candidate, it is called an X-Cycle.

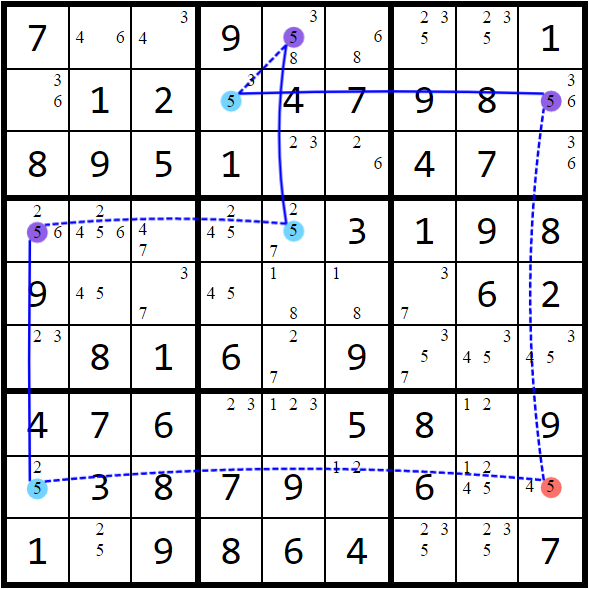
X-Cycle (candidate 5): If the red 5 was the solution to its cell (turned "on"), the blue and purple 5's around the chain would be alternatively turned "off" and "on" leading back to the red 5 being turned "off" - a contradiction, therefore it can be removed.

(Rule 2) If setting a strongly-linked chain to one of its two possible outcomes leads to a conflict elsewhere on the board, that entire chain must be set to its other possible outcome.

Here, a conflict means any impossible scenario on the board. For example, setting a chain to one of its possibilities could imply (1) a candidate appearing twice in a unit, (2) a candidate not appearing in a unit, (3) two different candidates both set in the same cell, or (4) a cell with no candidates in it. Since every strongly-linked chain only has two possibilities, a conflict arising with one possibility means that the chain must be set to its other possibility.

Invalid chain - When the red chain has the solid red candidates turned "on", it leads to several conflicts - here the solver finds that two 4's in the bottom row would both be turned "on". Therefore the red chain cannot be set to red - the solid red candidates can be removed and the solid green candidate is a solution.