Problem 59 - XOR decryption

XOR Ciphers

An XOR (exclusive-or) cipher is a common encryption technique where each character in a text is transformed using the XOR bitwise operator (⊕) and a key. In an XOR cipher, the XOR operator is used to transform a plaintext letter into its encrypted version. As a reminder, the XOR operator takes two binary inputs and outputs a 1 when the inputs are different and 0 when they are the same:

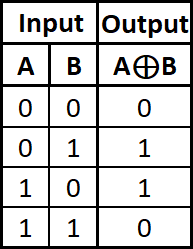
When A and B are binary numbers, A ⊕ B is done bit-by-bit. For example:

In an XOR cipher, both the plaintext and key are written in binary and combined using the XOR operator to form the cipher: plaintext ⊕ key = ciphertext. Because it is an associative operator, we can also say ciphertext ⊕ key = plaintext. If we have the cipher and can figure out the key, we can recover the original message.

As stated in the problem, when the key is as long as the plaintext, the encrypted ciphertext is unbreakable. Luckily we are given the information that the key is only 3 characters long and that all characters are lowercase letters. With 3 characters and 26 lowercase letters, there are 26³ = 17,576 possible keys to try. It's easy enough to programatically generate all of these keys and the corresponding plaintext for each; but how will we know which one is correct? It's not practical to manually read every possible plaintext to find the correct one. Fortunately, there is a technique to programatically determine the correct key.

Frequency Analysis

Frequency analysis leverages the fact that, in any language, certain letters are used more often than others. In English, the top 5 most common letters are commonly given as E, T, A, O, and I (depending on the source used). If we examine the ciphertext and look for the most common letter, we can guess that that letter represents E in the plaintext. Continuing down the list of most common letters, we can keep making guesses until patterns or recognizable words start to emerge.

While this is a popular method for pencil and paper solving, it has one main problem putting into use here - it still relies on guesswork. What we need is a way to quantitatively measure how likely any given substitution is.

One method used in cryptanalysis is to use the Chi-squared statistic to measure the probability of any given substitution. The Chi-squared statistic is given by:

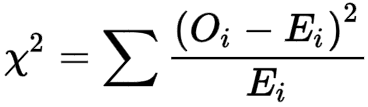
O_i is the count of occurences of the ith letter in a given distribution and E_i is the expected count of occurences of that letter. The closer the observed value O_i is to the expected value, the lower χ² will be and the more likely that letter follows the standard distribution of letters in the English language.

Implementation

Now that we have a way to determine the most likely key, we can start writing the functions needed to solve this problem. Since the χ² formula requires the expected and observed counts, we need a way to determine the expected counts.

#include <unordered_map>
#include <vector>
#include <fstream>
#include <cctype>	// isalpha, tolower
using Letter_Counts = std::unordered_map<unsigned char, double>;

Letter_Counts getExpected(unsigned dataLength) {
	static unsigned char letters[26] = {'a', 'b', 'c', 'd', 'e', 'f', 'g', 'h', 'i', 'j', 'k', 'l', 'm', 'n', 'o', 'p', 'q', 'r', 's', 't', 'u', 'v', 'w', 'x', 'y', 'z'};

	static double freqs[26] = {.0855, .016, .0316, .0387, .121, .0218, .0209, .0496, .0733, .0022, .0081, .0421, .0253, .0717, .0747, .0207, .001, .0633, .0673, .0894, .0268, .0106, .0183, .0019, .0172, .0011};

	Letter_Counts vals;
	for (unsigned i = 0; i < 26; i++)
		vals.emplace(letters[i], (dataLength * freqs[i]));
	return vals;
}               

The function getExpected accepts the number of letters in a given text as input and returns a map that contains the expected count of each individual letter (E_i in the above equation) using letter frequency data. For the function computing χ² we can use these expected counts in our computation.

double chiSquared(std::vector<unsigned char> text) {

	// count the observed frequency of letters
	Letter_Counts observed;
	unsigned numLetters = 0;
	for (auto c : text) {
		if (isalpha(c)) {
			observed[tolower(c)]++;
			numLetters++;
		}
	}
	// calculate the expected frequency of letters
	Letter_Counts expected = getExpected(numLetters);

	// calculate the chi-squared value of the text
	double chiSquared = 0.0;
	for (unsigned char c = 'a'; c <= 'z'; c++) {
		double degree = (observed[c] - expected[c]) * (observed[c] - expected[c]) / expected[c];
		chiSquared += degree;
	}
	return chiSquared;
}               

chiSquared takes a block of text as input (stored as a vector of characters) and returns the χ² value of that text. This value corresponds to how closely the input text matches the normal distribution of letters in the English language.

With these two functions we can write the rest of the code to decrypt the cipher. We first read the cipher text into a vector container:

std::vector<unsigned char> cipherText;
std::ifstream f(filename);
if (!f) {
	std::cerr << "Error opening cipher file\n";
	return 0;
}
std::string s;
while (getline(f, s, ',')) cipherText.push_back(static_cast<unsigned char>(std::stoul(s)));
f.close();      

Because we know the key is 3 characters long, we know that every 3rd character in the cipher will be encrypted using the same character of the key (the key is repeated to cover the length of the entire plaintext). For this reason we can break the ciphertext into 3 vectors representing each "column" of the ciphertext that correspond to each character of the key.

// key is 3 characters long, split the cipher into three columns
std::vector<std::vector<unsigned char>> cols(3);
int i = 0;
for (auto c : cipherText) {
	cols[i].push_back(c);
	if (++i > 2) i = 0;
}               

With this data we can now calculate the key one character at a time. This can be done by trying every lowercase letter and choosing the one whose corresponding plaintext produces the lowest value of χ².

// each character of the key corresponds to one column of the cipher
unsigned char key[3] = {};
int k = 0;
for (auto col : cols) {
	std::vector<unsigned char> plainCol;

	// try each char for this col and select the one that produces plaintext that most closely matches the letter frequencies of the English language
	double lowestChi = 1'000'000.0;
	unsigned char keyChar;
	for (char testChar = 'a'; testChar <= 'z'; testChar++) {
		plainCol.clear();
		for (auto c : col) plainCol.push_back(static_cast<unsigned char>(c ^ testChar));
		double chi = chiSquared(plainCol);
		if (chi < lowestChi) {
			lowestChi = chi;
			keyChar = testChar;
		}
	}

	key[k] = keyChar;
	k++;
}               

Finally, with this key, the original plaintext can be recovered and the result computed.

std::vector<unsigned char> plainText;
k = 0;
for (auto c : cipherText) {
	plainText.push_back(static_cast<unsigned char>(c ^ key[k]));
	if (++k > 2) k = 0;
}

// add the ascii values of the chars in the plaintext
unsigned result = 0;
for (auto c : plainText) result += c;

Final Thoughts

Although the Chi-squared test is not a perfect way to decrypt any XOR cypher it was enough to solve this problem. With longer plaintexts there would be more certainty of both the computed key and plaintext being correct. Improvements to this method could use more advanced techniques of frequency analysis that consider not only the most common letters in the English language, but also the most common pairs or larger groups of letters. For example, the letter Q is almost always followed by a U and the most common digraphs include TH, ER, ON, and AN.