Problem 95 - Amicable Chains
The proper divisors of a number are all the divisors excluding the number itself. For example, the proper divisors of 28 are 1, 2, 4, 7, and 14. As the sum of these divisors is equal to 28, we call it a perfect number.
Interestingly the sum of the proper divisors of 220 is 284 and the sum of the proper divisors of 284 is 220, forming a chain of two numbers. For this reason, 220 and 284 are called an amicable pair.
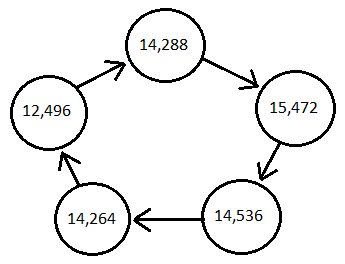
Perhaps less well known are longer chains. For example, starting with 12496, we form a chain of five numbers:
12496 → 14288 → 15472 → 14536 → 14264 (→ 12496 → ...)
Since this chain returns to its starting point, it is called an amicable chain.
Find the smallest member of the longest amicable chain with no element exceeding one million.
Starting with the Primes
This problem requires us to find the longest chain of amicable numbers. This means we can think about this in the context of graph theory and apply an appropriate algorithm to detect chains, or cycles, within a graph. However, before considering graph algorithms, we first have the problem of building the graph - that is, finding all of the amicable numbers.
I find that it's helpful to work through this problem in a bottom-up approach. First, we'll find an efficient way to generate all of the proper divisors of a number n. The simplest way to achieve this is by testing every number < n to see which are divisible by n. However, performing this for the required first million numbers will be very time consuming - on the order of n2 operations.
Instead, we can use a faster method that relies on the distinct prime factors of n. The sum of divisors (σ) of n is given by:
\(\sigma(n) = \prod\limits_{i=1}^{r}{\frac{p_i^{a_i+1}-1}{p_i-1}}\)
where
r = the number of distinct prime factors of n
pi = the ith prime factor
ai = the multiplicity of pi
Here, the multiplicity means the number of times pi divides n. Using this formula only requires finding the distinct prime factors of n rather than testing the divisibility of every number < n. For a large amount of numbers, this process can be sped up by pre-calculating the prime numbers.
Therefore, before implementing the above algorithm we need a function to generate prime numbers. An efficient way to do this is to use the Sieve of Eratosthenes.
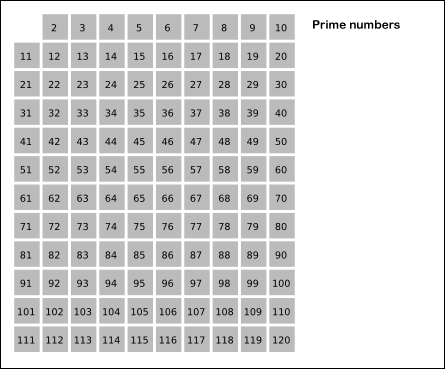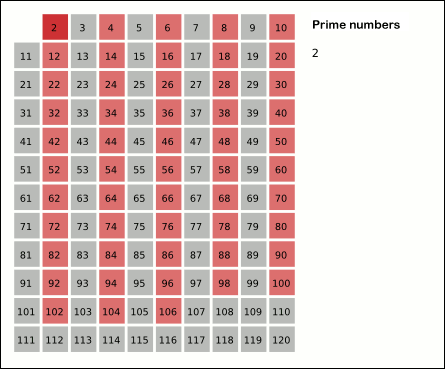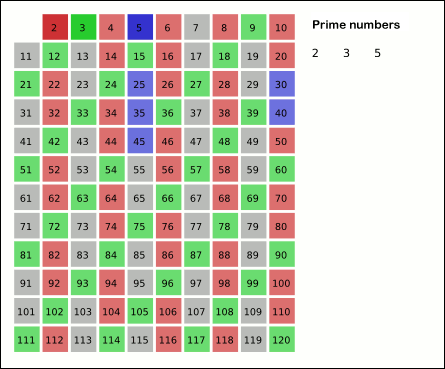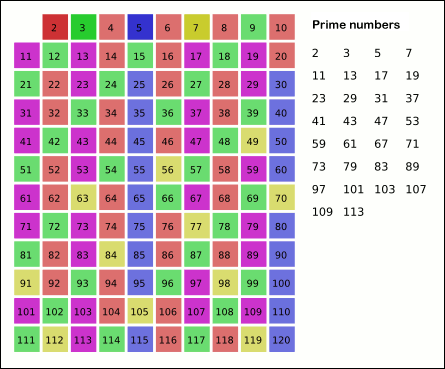
The sieve finds all prime numbers up to n by marking all multiples of primes as not prime and taking those remaining unmarked numbers as prime. Consider the function:
#include <vector>
std::vector<int> generatePrimes(int n) {
bool *primeSieve = new bool[n]();
for (int i = 2; i < n; i++) primeSieve[i] = true;
for (int i = 2; i*i < n; i++)
if (primeSieve[i])
for (int j = i*i; j < n; j += i)
primeSieve[j] = false;
std::vector<int> primes;
for (int i = 0; i < n; i++)
if (primeSieve[i]) primes.push_back(i);
delete[] primeSieve;
return primes;
}
This function returns a containing the prime numbers below n. The sieve is represented as an array of bools all initially set to . Multiples of primes (denoted with j in the inner loop) are marked . This implementation uses an optimization where you only need to check multiples of i starting from i2 as smaller multiples will have already been marked from smaller primes.
σ(n) and the Aliquot Sum
As mentioned above, the sum of divisors of n is given by:
\(\sigma(n) = \prod\limits_{i=1}^{r}{\frac{p_i^{a_i+1}-1}{p_i-1}}\)
where
r = the number of distinct prime factors of n
pi = the ith prime factor
ai = the multiplicity of pi
Using 220 as an example, we find that its proper divisors (all divisors not including 220 itself) are {1, 2, 4, 5, 10, 11, 20, 22, 44, 55, 110}. The sum of these proper divisors, also known as the Aliquot sum, is 284 as given in the problem.
If we instead consider the prime factors of 220,
\(220 = 2^2 \cdot 5 \cdot 11\)
the above formula gives
\(\sigma(220) = \frac{2^{2+1}-1}{2-1}\) \(\cdot\) \(\frac{5^{1+1}-1}{5-1}\) \(\cdot\) \(\frac{11^{1+1}-1}{11-1}\)
\(\sigma(220) = 7 \cdot 6 \cdot 12 = 504\)
To get the Aliquot sum we simply subtract out the number itself:
\(aliquot(220) = \sigma(220) - 220\)
\(aliquot(220) = 504 - 220 = 284\)
Using the primes we generated previously we can find the distinct factors of n by testing divisibility:
int num = n; // make a copy of n to reduce
int sigma = 1;
// Find the distinct prime factors of n up to sqrt(n)
for (auto p : primes) {
if (p*p > n) break;
if (n % p != 0) continue;
int m = p; // m = p^(a+1)
while (n % m == 0) // get the multiplicity of p
m *= p;
num /= (m/p); // reduce n at each step
sigma *= (m-1)/(p-1);
}
// If n is prime or has a prime factor > sqrt(n) it is a distinct prime factor with multiplicity of 1
if (num > 1) sigma *= (num+1);
aliquot[n] = sigma - n;I use an optimization where n (as the variable num) is divided by its prime factors as they are found. This means we only need to check primes up to \(\sqrt{n}\). If n has a prime factor > \(\sqrt{n}\), it will be leftover in num and is guaranteed to have a multiplicity of 1.
This optimization also means that the upper limit on primes we need to generate is \(\sqrt{1,000,000}\).
Building the Graph
Now that we have a method to generate all Aliquot sums, we can think about how to find chains of amicable numbers. Remember that amicable numbers are 2 numbers where each number has an Aliquot sum equal to the other number. Amicable chains extend this concept to >2 numbers. To start, think of the chain of 5 amicable numbers stated in the problem as forming a cyclic, directed graph like so:
Actually, the full graph implied by this problem includes a vertex for every number up to 1,000,000:
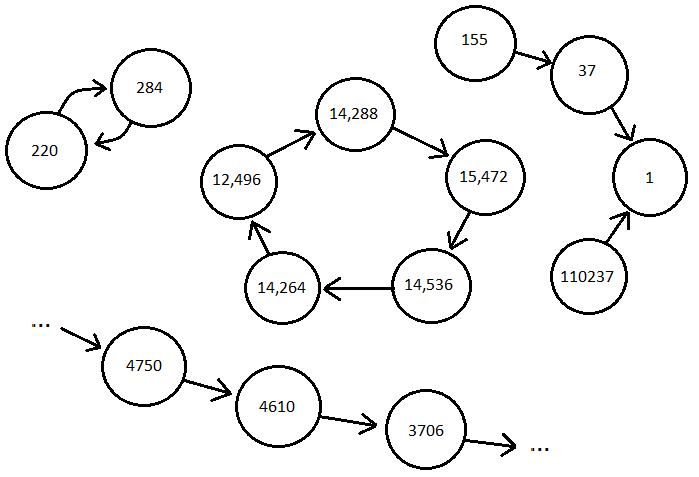
We can draw a few conclusions about this graph. Every vertex will have exactly one outgoing edge pointing to the value of its Aliquot sum. Every prime number vertex will have its edge pointing to 1 and the number 1 itself will point to 0 (which will be considered a dead end). There are V = 1,000,000 vertices and E = 1,000,000 edges which imply a relatively sparse graph.
This graph can be stored as an adjacency list where each list only contains one neighbor node (given by the Aliquot sum). A simple array containing the Aliquot sums of every number up to n = 1,000,000 is sufficient to serve as our graph's adjacency list.
Detecting Graph Cycles
A cycle in a graph consists of a path of at least 2 vertices where the the start and end vertices are the same (the term cycle will be synonymous with 'chain' stated in the problem). The algorithm I use to find all cycles in this directed graph is a modified depth-first search (DFS). First I'll define values to represent the processing state of a vertex:
enum class color {
white, // unvisited
grey, // visiting
black // visited
};and an array to represent which vertices need to be processed:
// initialize all vertices as white (unvisited)
std::vector<color> visited = std::vector<color>(N+1, color::white);
A recursive DFS function will check whether a given vertex belongs to a cycle. This function is described by the following pseudocode.
bool dfs(currVertex, vertices, visited, N, &cycle)
// return true if currVertex is part of a cycle, false if not
(1) If the current vertex has already been visited or is out of range
(i) Return false
(2) If the current vertex is a dead-end (leads to "1")
(i) Mark the current vertex as visited
(ii) Return false
(2) If the current vertex has been seen before
the current vertex is part of a cycle
(i) Add the current vertex to cycle
(ii) Mark the current vertex as visited
(iii) Return true
(3) The current vertex is unvisited, mark it as visiting
(4) Recursively call dfs on the current vertex's single neighbor
(i) If this call returns true and the current vertex is still marked as visiting
the current vertex is part of a cycle
(a) Add the current vertex to cycle
(b) Mark the current vertex as visited
(c) Return true
(i) Else
the current vertex is not part of a cycle
(a) Mark the current vertex as visited
(b) Return false
In the main function we call the recursive DFS function on every unvisited vertex and record when a discovered cycle is longer than the longest discovered so far.
int *aliquot; // graph adjacency list
std::vector<int> cycle, longestCycle;
for (int n = 2; n < N+1; n++) {
if (aliquot[n] == 1 || visited[n] == color::black)
continue;
dfs(n, aliquot, N+1, visited, cycle);
if (cycle.size() > longestCycle.size())
longestCycle = cycle;
cycle.clear();
}Implementation
Putting all the pieces together, this is the final implementation.
#include <vector>
#include <cmath> // std::sqrt
#include <algorithm> // std::min_element
#include <iostream> // std::cout
// unvisited, visiting, visited
enum class color { white, grey, black };
std::vector<int> generatePrimes(int N) {
bool *primeSieve = new bool[N]();
for (int i = 2; i < N; i++) primeSieve[i] = true;
for (int i = 2; i*i < N; i++)
if (primeSieve[i])
for (int j = i*i; j < N; j += i) primeSieve[j] = false;
std::vector<int> primes;
for (int i = 0; i < N; i++)
if (primeSieve[i]) primes.push_back(i);
delete[] primeSieve;
return primes;
}
void getAliquotSums(int *aliquot, int N, const std::vector<int> &primes) {
for (int n = 2; n < N; n++) {
int num = n; // make a copy of n to reduce
int sigma = 1;
// Find the distinct prime factors of n up to sqrt(n)
for (auto p : primes) {
if (p*p > n) break;
if (n % p != 0) continue;
int m = p; // m = p^(a+1)
while (n % m == 0) // get the multiplicity of p
m *= p;
num /= (m/p); // reduce n with each prime factor
sigma *= (m-1)/(p-1);
}
// If n is prime or has a prime factor > sqrt(n),
// it is a distinct prime factor with multiplicity of 1
if (num > 1) sigma *= (num+1);
aliquot[n] = sigma - n;
}
}
bool dfs(int curr, int *vertices, int N, std::vector<color> &visited, std::vector<int> &cycle) {
// Return true if the curr vertex is part of a cycle, false if not
// vertex is out of range, already visited, or a dead-end
if (curr >= N || visited[curr] == color::black) return false;
if (vertices[curr] == 1) { // dead-end
visited[curr] = color::black;
return false;
}
// vertex was seen before, cycle detected
if (visited[curr] == color::grey) {
cycle.push_back(curr);
visited[curr] = color::black;
return true;
}
// vertex is unvisited, mark as visiting
visited[curr] = color::grey;
// check the single neighbor of curr
if (dfs(vertices[curr], vertices, N, visited, cycle) && visited[curr] == color::grey) {
// the vertex that curr points to is part of a cycle
// and curr belongs to that cycle
cycle.push_back(curr);
visited[curr] = color::black;
return true;
} else {
// vertex is not part of a cycle, mark as visited
visited[curr] = color::black;
return false;
}
}
int longestAmicableChain(int N) {
// Generate all of the primes under sqrt(N)
std::vector<int> primes = generatePrimes(static_cast<int>(std::sqrt(N)));
// Get the aliquot sum for every number up to N
int *aliquot = new int[N+1]();
getAliquotSums(aliquot, N, primes);
// Find every cycle and record the longest one
std::vector<color> visited = std::vector<color>(N+1, color::white);
std::vector<int> cycle, longestCycle;
for (int n = 2; n < N+1; n++) {
if (aliquot[n] == 1 || visited[n] == color::black)
continue;
dfs(n, aliquot, N+1, visited, cycle);
if (cycle.size() > longestCycle.size())
longestCycle = cycle;
cycle.clear();
}
delete[] aliquot;
if (longestCycle.empty()) return 0; // no cycle found
// Print chain
std::cout << "Chain of length " << longestCycle.size() << " found:\n";
for (auto it = longestCycle.rbegin(); it != longestCycle.rend(); ++it)
std::cout << *it << "->";
std::cout << longestCycle.back() << "\n";
return *std::min_element(longestCycle.begin(), longestCycle.end());
}