Problem 64 - Odd period square roots

All square roots are periodic when written as continued fractions and can be written in the form:
$\displaystyle \quad \quad \sqrt{N}=a_0+\frac 1 {a_1+\frac 1 {a_2+ \frac 1 {a3+ \dots}}}$
For example, let us consider $\sqrt{23}:$
$\quad \quad \sqrt{23}=4+\sqrt{23}-4=4+\frac 1 {\frac 1 {\sqrt{23}-4}}=4+\frac 1 {1+\frac{\sqrt{23}-3}7}$
If we continue we would get the following expansion:
$\displaystyle \quad \quad \sqrt{23}=4+\frac 1 {1+\frac 1 {3+ \frac 1 {1+\frac 1 {8+ \dots}}}}$
The process can be summarised as follows:

$\quad \quad a_0=4, \frac 1 {\sqrt{23}-4}=\frac {\sqrt{23}+4} 7=1+\frac {\sqrt{23}-3} 7$
$\quad \quad a_1=1, \frac 7 {\sqrt{23}-3}=\frac {7(\sqrt{23}+3)} {14}=3+\frac {\sqrt{23}-3} 2$
$\quad \quad a_2=3, \frac 2 {\sqrt{23}-3}=\frac {2(\sqrt{23}+3)} {14}=1+\frac {\sqrt{23}-4} 7$
$\quad \quad a_3=1, \frac 7 {\sqrt{23}-4}=\frac {7(\sqrt{23}+4)} 7=8+\sqrt{23}-4$
$\quad \quad a_4=8, \frac 1 {\sqrt{23}-4}=\frac {\sqrt{23}+4} 7=1+\frac {\sqrt{23}-3} 7$
$\quad \quad a_5=1, \frac 7 {\sqrt{23}-3}=\frac {7 (\sqrt{23}+3)} {14}=3+\frac {\sqrt{23}-3} 2$
$\quad \quad a_6=3, \frac 2 {\sqrt{23}-3}=\frac {2(\sqrt{23}+3)} {14}=1+\frac {\sqrt{23}-4} 7$
$\quad \quad a_7=1, \frac 7 {\sqrt{23}-4}=\frac {7(\sqrt{23}+4)} {7}=8+\sqrt{23}-4$

It can be seen that the sequence is repeating. For conciseness, we use the notation $\sqrt{23}=[4;(1,3,1,8)]$, to indicate that the block (1,3,1,8) repeats indefinitely.

The first ten continued fraction representations of (irrational) square roots are:

$\quad \quad \sqrt{2}=[1;(2)]$, period=$1$
$\quad \quad \sqrt{3}=[1;(1,2)]$, period=$2$
$\quad \quad \sqrt{5}=[2;(4)]$, period=$1$
$\quad \quad \sqrt{6}=[2;(2,4)]$, period=$2$
$\quad \quad \sqrt{7}=[2;(1,1,1,4)]$, period=$4$
$\quad \quad \sqrt{8}=[2;(1,4)]$, period=$2$
$\quad \quad \sqrt{10}=[3;(6)]$, period=$1$
$\quad \quad \sqrt{11}=[3;(3,6)]$, period=$2$
$\quad \quad \sqrt{12}=[3;(2,6)]$, period=$2$
$\quad \quad \sqrt{13}=[3;(1,1,1,1,6)]$, period=$5$

Exactly four continued fractions, for $N \le 13$, have an odd period.

How many continued fractions for $N \le 10\,000$ have an odd period?

Simple Continued Fractions

Before tackling this problem it's necessary to understand continued fractions and their notation. In the most basic terms, a continued fraction is a way of writing fractions that include nested fractions such as:

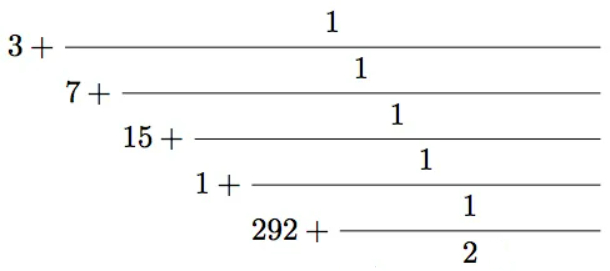
$continued-fraction$

They are commonly used as a way to represent rational numbers. For example, consider the rational number 415/93. A normal decimal approximation may be rounded and given as 4.4624. Instead, we can represent the number as a continued fraction by using an iterative process of repeated division. At each iteration we will perform Euclidean division to get an integer quotient and then use that to find the fractional remainder. The first iteration gives:

$\frac{415}{93} = 4 + \frac{43}{93}$

For each subsequent iteration, take the reciprocal of the fractional remainder and repeat the above division. The next few iterations are:

$\frac{93}{43} = 2 + \frac{7}{43}$

$\frac{43}{7} = 6 + \frac{1}{7}$

$\frac{7}{1} = 7 + 0$ (iteration stops)

At each step we are approximating the value of the previous fraction with (the reciprocal of) an integer. For instance:

$\frac{415}{93} \approx 4$

$\frac{43}{93} \approx$ (the reciprocal of) $2$

$\frac{7}{43} \approx$ (the reciprocal of) $6$

$\frac{1}{7} = $ (the reciprocal of) $7$

We can use these integer approximations to write our continued fraction representation as:

$\frac{415}{93} = 4 + \frac{1}{2 + \frac{1}{6 + \frac{1}{7}}}$

This form of continued fraction where every numerator is 1 is called a simple continued fraction or said to be in canonical form. Since all of the numerators are the same, another more concise way to write simple continued fractions (using the above as an example) is:

$\frac{415}{93} = [4; 2, 6, 7]$

Those integer values (4, 2, 6, 7) are called the coefficients of the continued fraction.

Periodic Continued Fractions

When a continued fraction terminates (as in the above example) it is called a finite continued fraction. In addition to finite continued fractions, there are periodic continued fractions that don't terminate but instead repeat indefinitely. It's been shown that every irrational square root can be represented as a periodic continued fraction. Take for example $\sqrt{3}$. As given by the problem, $\sqrt{3}$ has the following continued fraction representation:

$\sqrt{3} = [1; (1, 2)] = [1; 1, 2, 1, 2, 1, 2, ...]$

where the parentheses indicate that the coefficients 1 and 2 repeat indefinitely. This continued fraction has a period of length 2.

So then the crux of the problem is finding and implementing an iterative algorithm, analagous to the one above, that gives us the periodic continued fraction of square roots. One such algorithm is as follows:

$\sqrt{S} = [a_0; a_1, a_2, ...]$

(1) Initialize $p_0 = 0, q_0 = 1, a_0 = \lfloor\sqrt{S}\rfloor$

(2) $p_{n+1} = q_na_n - p_n$

(3) $q_{n+1} = \frac{(S - p_{n+1}^2)}{q_n}$

(4) $a_{n+1} = \lfloor\frac{(a_0 + p_{n+1})}{q_{n+1}}\rfloor$

(5) Increment n and go back to (2)

This algorithm can be demonstrated with the example given in the problem. In each iteration we are splitting the current value into an integer and a fraction part. The integer becomes the coefficient a_n of that iteration and the inverse of the fraction part becomes the value for the next iteration. This has the effect of producing finer and finer approximations of our initial number.

For example, the first iteration of $\sqrt{23}$ is

Split $\sqrt{23}$ into an integer part and a fraction part:

$\sqrt{23} \approx 4$ (integer part, $a_0$)

the amount left over is $\sqrt{23}-4$ (fraction part)

Take the inverse of the fraction part and simplify:

$\frac{1}{\sqrt{23}-4} \cdot \frac{\sqrt{23}+4}{\sqrt{23}+4} = \frac{\sqrt{23}+4}{23-16} = \frac{\sqrt{23}+4}{7}$

Taking $\frac{\sqrt{23}+4}{7}$ as our new value, this is the second iteration:

Split $\frac{\sqrt{23}+4}{7}$ into an integer part and a fraction part:

we've already seen that $\sqrt{23}\approx4$, so using this approximation,

$\frac{\sqrt{23}+4}{7} \approx \frac{4+4}{7} \approx 1$ (integer part, $a_1$)

and the amount left over is $\frac{\sqrt{23}+4}{7}-1$ (fraction part)

Simplify and take the inverse of the fraction part:

$\frac{\sqrt{23}+4}{7}-1 = \frac{\sqrt{23}+4}{7}-\frac{7}{7} = \frac{\sqrt{23}-3}{7} \rightarrow \frac{7}{\sqrt{23}-3}$ (inverse)

For irrational square roots, this process will repeat forever. One key insight that helps us detect when to stop this algorithm is given by mathematician Évariste Galois. One of the derived results of his papers states that

$\sqrt{S} = [a_0; (a_1, a_2, ..., a_2, a_1, 2a_0)]$

This says that every irrational square root, S, will have a periodic continued fraction representation whose coefficients form a palindrome after a₀ and contain a final coefficient of twice a₀. For further reading on the math leading to this result, a good place to start is the wiki page on Periodic continued fractions. However, for our purposes, this observation tells us that we can terminate the algorithm when we run into a coefficient a_n that is equal to 2*a₀.

Implementation


                    int numOddPeriods(int N) {
	int count = 0;
	for (int n = 2; n <= N; n++) {
		int a0 = (int)sqrt(n);
		if (a0*a0 == n) continue;
		int p = 0, q = 1, a = a0, periodLength = 0;
		do {
			p = a*q - p;
			q = (n - p*p) / q;
			a = (a0 + p) / q;
			periodLength++;
		} while (a != 2*a0);
		if (periodLength%2) count++;
	}
	return count;
}

In the outer loop we check all of the integers up to 10,000 and increment count when an integer has an odd period length. In the inner while loop is the implementation of the algorithm listed above. This function makes use of the fact that in C++ positive integer division results in truncation of the quotient.

Previous: Powerful digit counts Next: Singular integer right triangles