Problem 75 - Singular integer right triangles

Pythagorean Triples

When dealing with right angle triangles, it's always a good idea to start with the reliable Pythagorean theorem:

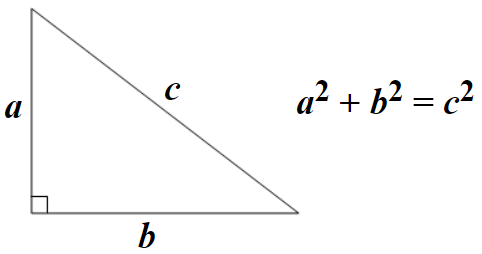
A solution to the Pythagorean theorem where a, b, and c are all integers is called a Pythagorean triple. We can see that all of the examples given in the problem are Pythagorean triples and it's clear that the problem is asking us to find all Pythagorean triples up to a limit. However, there is one catch, we are to not include any Pythagorean triples whose sum is equal to another Pythagorean triple. We'll come back to that detail later, for now we just need to find a method to generate triples.

Generating Triples

A quick online search shows many different ways to generate Pythagorean triples. For reference, let's call a triple {a, b, c}. One of the oldest and most well known methods, called Euclid's formula, produces triples by starting with two arbitrary positive integers, m and n, and uses the following formulas

a = m2 - n2
b = 2mn
c = m2 + n2

However we run into a problem with this method quickly. We've simply reduced the problem from generating arbitrary sets of 3 numbers, a, b, and c, to generating arbitrary sets of 2 numbers, m and n. In addition, these formulas must be modified with a third parameter, k, to generate all triples uniquely.

For m and n coprime and exactly one of which is even:
a = k * (m2 - n2)
b = k * (2mn)
c = k * (m2 + n2)

The introduction of k is required to produce the non-primitive triples. A primitive Pythagorean triple is one where a, b, and c are all coprime. For example {3, 4, 5} is a primitive triple but {9, 12, 15} is not because {9/3, 12/3, 15/3} = {3, 4, 5}.

Although this modified version of Euclid's formula is sufficient to solve this problem, it still requires us to produce all coprime integers m and n, not a trivial task. It may be worth looking at other methods.

Ternary Tree Method

A more recent discovery shows an interesting relationship among all primitive Pythagorean triples. The set of all primitive Pythagorean triples has the structure of a ternary tree - each primitive triple can be shown to have exactly 3 "descendant" primitive triples with the root of the tree being the triple {3, 4, 5}.

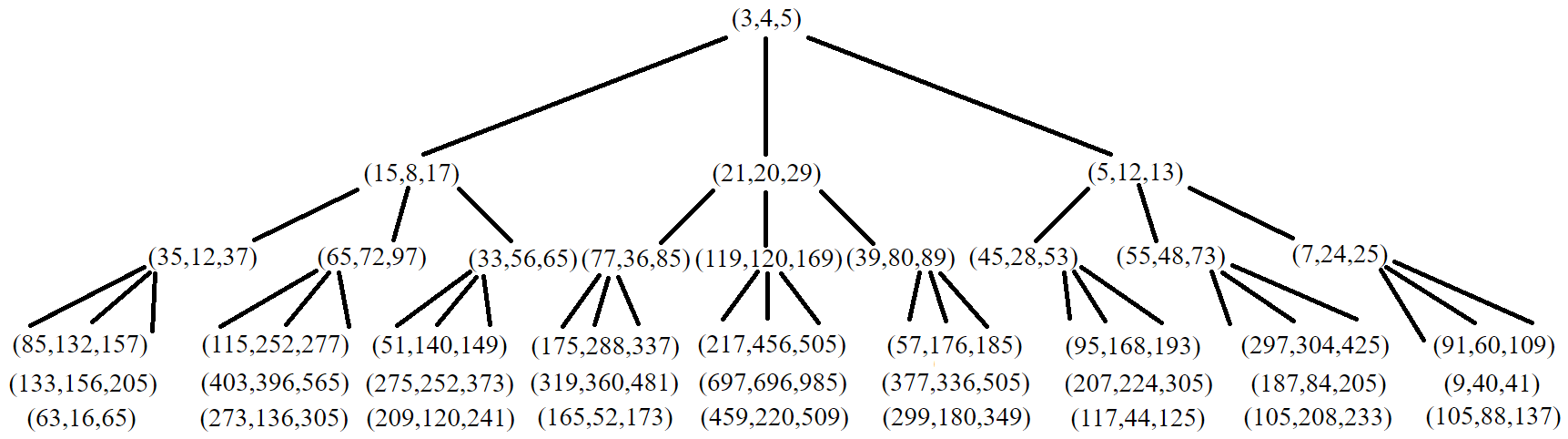
Given a node on the tree with values {a, b, c}, its three children nodes, A, B, and C, can be generated with the following matrix multiplications:

This method of generating triples has the property that every descendant triple will have a larger sum than its parents. Using this fact, we can perform a depth-first traversal of the tree that traverses down each branch until the sum of the generated triples exceeds the problem's limit of 1,500,000. This will allow us to cleanly generate all of the primitive Pythagorean triples. All that's left to do to generate the remaining non-primitive triples is to multiply each primitive triple by a multiple k.

Implementation

First, starting with a simple struct to represent a Pythagorean triple:

struct pyTriple {
	int a;
	int b;
	int c;
};              

This recursive function performs a depth-first traversal of the tree and the matrix multiplications listed above to generate all triples:

void generateTriples(pyTriple node, int *sumCount, int maxSum) {

	int sum = node.a + node.b + node.c;

	// The sum of a node's children will always be larger, stop traversing the tree
	if (sum > maxSum) return;

	// Record the sum of this primitive triple and all its multiples
	int k = 1;
	while (k*sum < maxSum) sumCount[sum*k++]++;

	// Generate the three children of this node, all of which are primitive
	pyTriple leftChild;
	leftChild.a     =  1*node.a + -2*node.b + 2*node.c;
	leftChild.b     =  2*node.a + -1*node.b + 2*node.c;
	leftChild.c     =  2*node.a + -2*node.b + 3*node.c;
	generateTriples(leftChild, sumCount, maxSum);

	pyTriple middleChild;
	middleChild.a   =  1*node.a +  2*node.b + 2*node.c;
	middleChild.b   =  2*node.a +  1*node.b + 2*node.c;
	middleChild.c   =  2*node.a +  2*node.b + 3*node.c;
	generateTriples(middleChild, sumCount, maxSum);

	pyTriple rightChild;
	rightChild.a    = -1*node.a +  2*node.b + 2*node.c;
	rightChild.b    = -2*node.a +  1*node.b + 2*node.c;
	rightChild.c    = -2*node.a +  2*node.b + 3*node.c;
	generateTriples(rightChild, sumCount, maxSum);
}               

Rather than recording the values of each triple, we are only interested in a triple's sum. sumCount is an array whose index represents a Pythagorean triple sum. The value at each index corresponds to the number of triples with that sum.

Finally, to account for the problem's specification to only count unique sums, we just need to perform one final step of iterating through sumCount to only count sums that appear exactly once. Note that we can increment the loop by 2 as every Pythagorean triple will have an even sum.

int numSinglePythagoreanTripleSums(int maxSum) {
	int *sumCount = new int[maxSum+1]();
	generateTriples({3, 4, 5}, sumCount, maxSum);   // initial node of the tree is the triple {3, 4, 5}
	int count = 0;
	for (int sum = 12; sum <= maxSum; sum += 2)
		if (sumCount[sum] == 1) count++;
	delete[] sumCount;
	return count;
}