Problem 83 - Path sum: four ways

Modeling the Graph

This problem calls for a shortest-path algorithm. In order to choose one, consider the graph implied by the given matrix. We can think of the 80x80 matrix as a weighted, directed graph consisting of 80x80 = 6400 vertices. Because the problem allows movement to adjacent vertices (above, below, and to either side), each vertex (except edge vertices) will have 4 edges to 4 neighbors. The cost (or weight) associated with each edge is the integer value of the destination vertex. For this reason, the graph will have directed edges, as travel between 2 neighboring vertices will have different costs depending on which direction you travel.

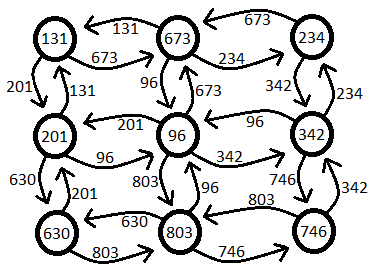
Since the problem specifies a single source vertex (top-left) and a single destination vertex (bottom-right), I chose Dijkstra's algorithm for its relative simplicity and acceptable time complexity. A faster algorithm, such as A*, could also be used.

Dijkstra's Shortest Path Algorithm

Dijkstra's algorithm makes use of several data structures. A graph, G, represents a structure to store all of the vertices. An array, D, stores the tentative shortest distance between a vertex v and the starting vertex. A priority queue, Q, is typically used to process vertices. In some implementations, an array, P, can be used to store the previous vertex in the tentative shortest path for any vertex in the graph. This can then be reconstructed once the shortest path is found to show the steps of the path. I do not use this structure for this problem.

The priority queue, Q, will hold vertices currently being processed and order them using their minimum distance in D. The vertex with the lowest distance recorded in D will have the highest priority and be placed at the front of the queue.

(1) Initialize:
		D[n] = INFINITY for every vertex n in G
		D[source] = 0
(2) Add source vertex to Q
(3) Remove the minimum vertex, u, from Q
(4) If (u == destination) go to (7)
(5) For each neighbor v of u
	(i) alt = D[u] + cost(v)
	(ii) if (alt < D[v])
			D[v] = alt
			Add v to Q
(6) If Q is not empty go to (3)
(7) Return D[destination]

Implementation

The graph of vertices, G, will be stored in a one-dimensional array where the index of each vertex will correspond to its row and column within the matrix using the following formula:

index = row*(total # rows) + column

For example, the cell marked 956 in the problem will have an index of 3*80 + 4 = 244 and a value of 956. The value of G[v] for vertex v will also correspond to the cost to travel to v from any of its neighbors.

First, a function to read the text file into G:

#include <string>
#include <sstream>
#include <fstream>

void readMatrix(std::string file, int *G, const int N) {
	std::ifstream f(file);
	if (!f) {
		std::cerr << "Error opening file";
		return;
	}
	for (int x = 0; x < N; x++) {
		// Rows separated by '\n'
		std::string buff;
		f >> buff;
		std::stringstream row(buff);
		for (int y = 0; y < N; y++) {
			// Cols separated by ','
			std::string val;
			std::getline(row, val, ',');
			G[x*N+y] = std::stoi(val);
		}
	}
}

Next, a function implementing Dijkstra's algorithm described above:

#include <queue>	// std::priority_queue

int dijkstraFourWays(int source, int destination, int *cost, const int N) {

	// Distance to each node from the source node
	int *dist = new int[N*N]();
	for (int i = 0; i < N*N; i++)
		dist[i] = INT_MAX;
	dist[source] = cost[source];	// source node

	// Min-priority queue with custom comparison fnc
	auto comp = [&dist](int lhs, int rhs) -> bool {
		return dist[lhs] > dist[rhs];
	};
	std::priority_queue<int, std::vector<int>, decltype(comp)> Q(comp);

	Q.push(source);
	while (!Q.empty()) {
		int u = Q.top();
		Q.pop();
		if (u == destination) break;
		int row = u / N, col = u % N;
		int neighbors[4] = {col+1 < N ? u+1 : -1,	// right
							col-1 >= 0 ? u-1 : -1,	// left
							row+1 < N ? u+N : -1,	// bottom
							row-1 >= 0 ? u-N : -1};	// top
		for (int i = 0; i < 4; i++) {
			int v = neighbors[i];
			if (v != -1) {
				int alt = dist[u] + cost[v];
				if (alt < dist[v]) {
					dist[v] = alt;
					Q.push(v);
				}
			}
		}
	}
	int result = dist[destination];
	delete[] dist;
	return result;
}

The arguments source and destination are the indices of the source and destination vertices. cost is the graph, G, as described above. N is the size of the matrix, in this problem, 80. dist is the array, D, of shortest distances described above.

I use the C++ std::priority_queue with a custom comparator lambda that compares the shortest distances using dist. I find the indices of the 4 neighbors of each vertex by using simple arithmetic between indices. A value of -1 is used if vertex u is on the edge of the graph and doesn't have that specific neighbor.

Finally, the driver function to find the shortest path:

int shortestPath(std::string file, const int N) {

	// Read the data
	int *graph = new int[N*N]();
	readMatrix(file, graph, N);

	// Find the shortest path from top left (0, 0) to bottom right (N-1, N-1)
	int result = dijkstraFourWays(0, N*N-1, graph, N);

	delete[] graph;
	return result;
}