Problem 76 - Counting summations

Partitions

In number theory, a partition of a positive integer is a way of writing that integer as a sum of at least 2 other positive integers. For example, the problem lists the six partitions of the number 5. In writing partitions, order does not matter; 4 + 1 is the same partition as 1 + 4. The partition function, p(n), gives the number of partitions of n. In this problem we need to find the value of p(100).

Although there is no closed-form expression for p(n), mathematician Leonhard Euler (of this project's namesake) proved an identity called the Pentagonal number theorem that leads directly to a recurrence relation for p(n). The following few sections briefly describe the derivation of this recurrence relation to calculate p(100). To see the final equation skip to Implementation.

Pentagonal Number Theorem

Pentagonal numbers are numbers of the form

where n gives the nth pentagonal number. The first few are 1, 5, 12, 22, 35. They are called pentagonal because the nth pentagonal is the number of dots needed to form a pentagon with n sides.

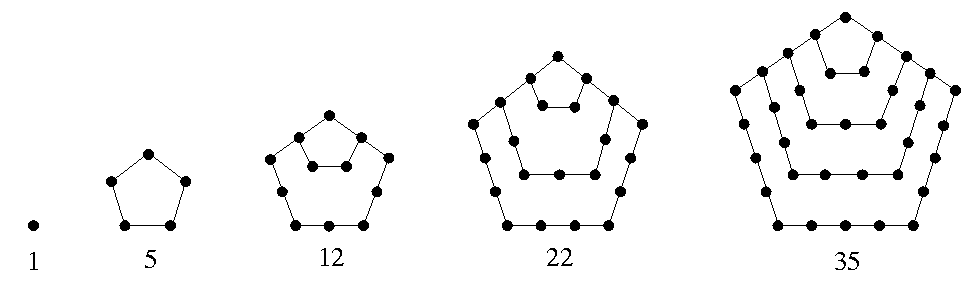
When negative values of n in the above formula are allowed, the generalized pentagonal numbers are obtained. For n = 0, 1, -1, 2, -2, 3, -3; the first several generalized pentagonal numbers are 0, 1, 2, 5, 7, 12, 15.

The Pentagonal number theorem shows an important connection between products and series. Euler found that the infinite product:

is equivalent to the infinite series:

The exponents of this series are precisely the generalized pentagonal numbers, hence the theorem's name. Writing the formal definition, the theorem states

A Generating Function for p(n)

In order to find a suitable algorithm for the partition function, let's start with a generating function for p(n). A generating function is a power series whose coefficients form a sequence of a numbers. For example, the Fibonacci sequence (0, 1, 1, 3, 5, 8, 13, ...) can be represented by the power series

Note how the coefficient of the nth term gives the nth Fibonacci number (e.g. the 6th Fibonacci number, 13, is given by the coefficient of x⁶). The above power series is then written as the generating function:

where F_n is the nth Fibonacci number and the expression on the right is the generating function's closed form.

What we want is a generating function for p(n), where the coefficient of the nth term gives the number of partitions for the nth integer. To find a generating function for p(n), consider the following infinite product:

Each factor represents an integer. The second factor, \((1+x^2+x^4+x^6+...)\), also written as \((1+(x^2)^1+(x^2)^2+(x^2)^3)\), represents the integer 2. Each term in this factor represents the quantity of 2's that we can choose when creating a partition. For example \(x^6\) represents choosing three 2's (\(x^6\ = x^2x^2x^2\)).

When this entire product is multiplied out, we pick one term from each factor in all possible ways. For example, if we pick x³ from the first factor, x² from the second factor, x¹⁵ from the fifth factor, and 1's from all the other factors, this would multiply out to x²⁰. This term would correspond to picking three 1's (\(x^3\ = x^1x^1x^1\)), one 2 (\(x^2\ = x^2\)), and three 5's (\(x^{15}\ = x^5x^5x^5\)). This is a partition of 20: 1 + 1 + 1 + 2 + 5 + 5 + 5 = 20.

When multiplying all of the factors in all possible ways, all possible combinations of partitions would be generated. The product is written as

Because we know that the geometric series converges,

we can then substitute the sum in the above product to get

Therefore, the generating function for p(n) is

A Recurrence Relation for p(n)

Unlike the Fibonacci example earlier, the generating function for p(n) is not known to have a closed form representation. However, using the generating function and Euler's pentagonal theorem, we can show a recurrence relation (a recursive definition) that will allow us to calculate p(n) exactly.

Starting with the generating function:

From the Pentagonal number theorem we can replace the infinite product \(\prod\limits_{n=1}^{\infty}({1-x^n})\) with the infinite sum \(\sum\limits_{k=-\infty}^{\infty}(-1)^kx^{g(k)}\) derived previously:

Expanding both infinite sums:

As the only term in the left factor with no x, p(0) must = 1 for this equality to hold, therefore

When the left side of this equation is multiplied out, each power of x will have some coefficient a_n

Thus for \(n≥1\), the coefficient a_n must = 0.

Consider again the equality:

To find, for example, the resulting coefficient, a₁₀, for x¹⁰ once the equation is multiplied out, it's important to recognize that only certain combinations of terms can be multiplied together to produce x¹⁰. For example,

These terms all contribute to a₁₀.

Rearranging to solve for p(10), we find the following recurrence relation:

More generally, the recurrence relation to calculate p(n) for any n is:

Implementation

First I use a recursive function to implement the recurrence relation above.

int countPartitions(int *p, int n) {
	if (n < 0) return 0;
	if (p[n]) return p[n];
	int count = 0, k = 1, gk = 1;
	while (n - gk >= 0) {
		count += countPartitions(p, n-gk) * (k % 2 == 0 ? -1 : 1);
		k *= -1;
		if (k > 0) k++;
		gk = (k*(3*k-1)) / 2;
	}
	p[n] = count;
	return count;
}

This function uses the base cases p(0) = 1 and p(n) = 0 for any n < 0. In addition, I found it necessary to cache the value of each partition found in array p. In order to calculate all of the generalized pentagonal numbers, I use the lines

k *= -1;
if (k > 0) k++;
gk = (k*(3*k-1)) / 2;

This produces the following iterations of k: 1, -1, 2, -2, ... and the corresponding pentagonal numbers gk.

Finally, the driver function to produce the value of p(n):

int numPartitions(int n) {
    int *p = new int[n+1]();
    p[0] = 1;   // base case
    int result = countPartitions(p, n);
    delete[] p;
    return result-1;
}

Important to note: the problem's wording specifically asks for the number of partitions having at least 2 terms. The recurrence method I used to calculate the number of partitions includes the singular partition (100). Therefore, a final subtraction by 1 is necessary to produce the correct answer of 190,569,291 ways to partition 100 into at least 2 integers.