Digital Audio
A study of digital audio and digital signal processing theory. Topics included discrete time sampling, quantization, dithering, analog/digital conversion, signal modulation, digital filtering, and convolution and the Fourier transform. Labs were performed using Matlab.
Labs
-
Lab 1 - MATLAB Fundamentals and Sinusoidal Synthesis
ReportIn this lab we learned the basics of MATLAB by creating sinusoids, combining multiple sinusoids, and plotting them. We also learned how to import external audio files.
440Hz tone summed with another audio file -
Lab 2 - Sampling, Quantization, and Dither
ReportIn this lab we explored the concepts of sampling rates, aliasing, and quantization. We used a function to examine a sine wave quantized to 8, 4, and 2 bits. We also used quantization and random noise to demonstrate the benefits of dither.
100Hz-5kHz sine sweep with a sample rate of 4kHz 100Hz-5kHz sine sweep with a sample rate of 10kHz -
Lab 3 - Amplitude and Frequency Modulation
ReportHere we explored the concepts and uses of amplitude modulation (AM) and frequency modulation (FM).
Part 1c - An example of AM (tremolo) Part 2d - An example of FM (vibrato) -
Lab 4 - Basic Filtering
ReportIn this lab we began basic filtering operations using the difference equation of a first-order feed-forward filter. We listened to the filtered audio file and plotted the waveform and magnitude spectrum.
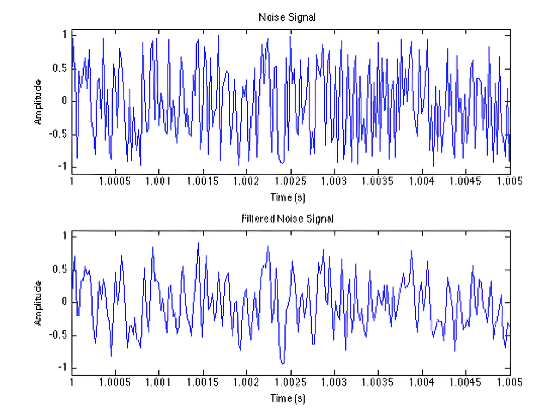
The effects of a 1st order LPF on a waveform of noise 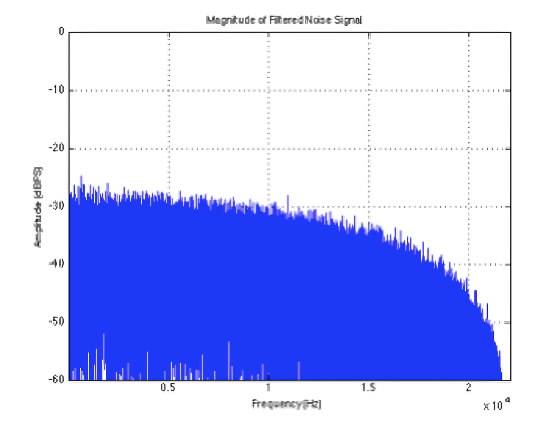
The magnitude response of the filtered noise signal -
Lab 5 - Resonant Filter Analysis/Design with MATLAB
Report
CodeIn this lab we continued on to more advanced filter design by designing a second-order feedback filter and a second-order resonant filter. The resonant filter was designed to have a cutoff frequency of 2000Hz and a bandwidth of 1000Hz.
Part 2c - The original unfiltered .wav file A .wav file put through a second-order resonant filter 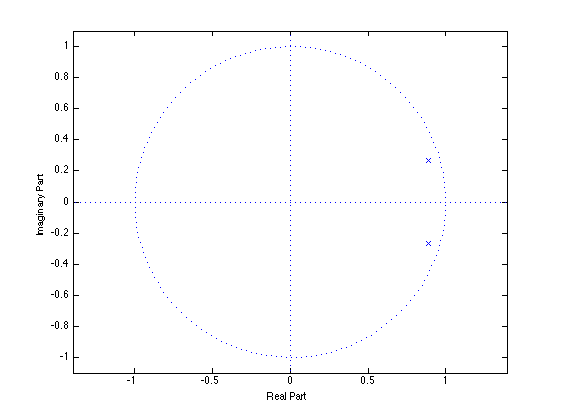
Part 2a - Pole-Zero Plot of the resonant filter 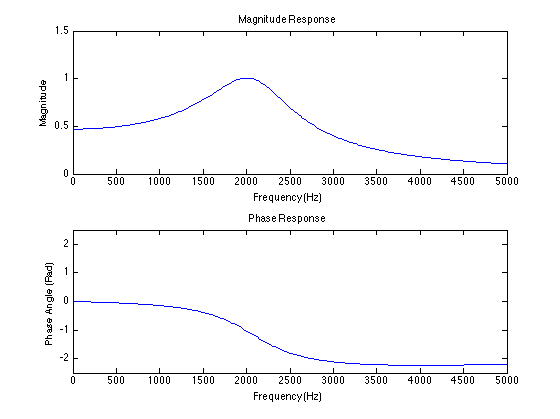
Part 2a - Magnitude-Phase Plot of the resonant filter -
Lab 6 - Karplus-Strong String Model
Report
Code
Karplus-Strong FunctionThis lab explored the Plucked String Karplus-Strong Model - a form of digital synthesis of a plucked string. The aim of this lab was to implement the K-S filter's difference equation and play an impulse and noise signal through it. The resulting sound should resemble a plucked string.
An impulse being filtered through the K-S filter 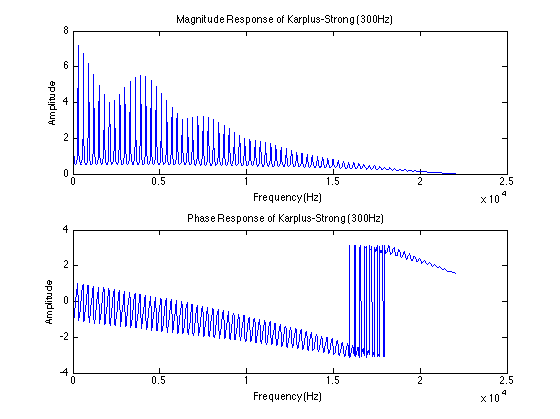
The magnitude and phase response of the K-S filter. 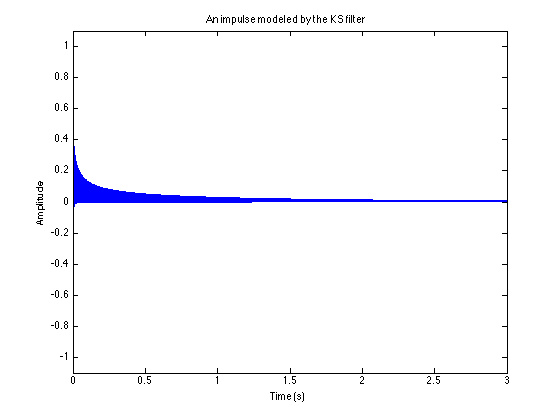
Part 4 - The impulse response of the K-S filter 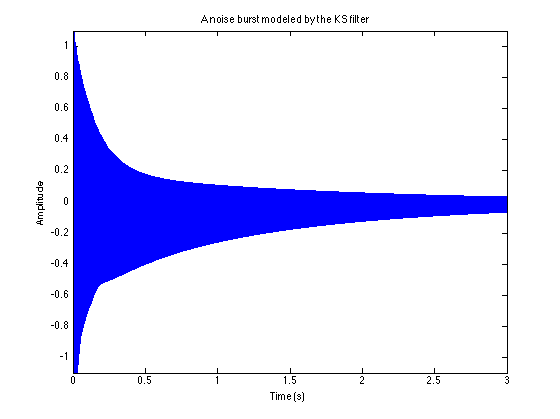
Part 5 - Noise filtered through the K-S filter -
Lab 7 - Convolution and the FFT
Report
CodeThis lab focused on convolution and also began discussion on the Discrete Fourier Transform (DFT). We wrote our own two convolution functions. The first function manually performed convolution by summing an input signal with an impulse response of a space. The second function performed convolution by utilizing the Fast Fourier Transform (FFT) and Convolution Theorem - the input signal and impulse response underwent the FFT, were multiplied together, then underwent the inverse FFT. This works because performing the FFT on a signal takes that signal from the time domain to the frequency domain and convolution in the time domain is equivalent to multiplication in the frequency domain (convolution theorem). We compared the two methods by convolving a short snare hit with a room's impulse response and timing how long each method took.
Manual Convolution - Time taken: 306.18s
Convolution using the FFT - Time taken: 0.0163s -
Lab 8 - Filtering Using the FFT
Report
Code
Feedback Suppression FilterIn this lab we began using the FFT to filter signals. We created a feedback suppression system that would locate the unwanted sinusoid component (caused by audio feedback) in a signal and then remove it while leaving the rest of the signal intact. For this lab we read in a .wav file and added simulated audio feedback to the file by "injecting" a 4000Hz sinusoid. We then wrote a function that would filter out this 4000Hz frequency from the file by using the FFT.
A .wav file with a 4kHz feedback frequency added The filtered .wav file with the feedback removed